Risk Measures

Quickstart

outcomes = rand(100)

# direct usage
VaR(0.90)(outcomes) # ≈ 0.90  
CTE(0.90)(outcomes) # ≈ 0.95  
WangTransform(0.90)(outcomes) # ≈ 0.81

# construct a reusable object (functor)
rm = VaR(0.90)

rm(outcomes) # ≈ 0.90

Introduction

Risk measures encompass the set of functions that map a set of outcomes to an output value characterizing the associated riskiness of those outcomes. As is usual when attempting to compress information (e.g. condensing information into a single value), there are multiple ways we can characterize this riskiness.

Coherence & Other Desirable Properties

Further, it is desirable that a risk measure has certain properties, and risk measures that meet the first four criteria are called "Coherent" in the literature. From "An Introduction to Risk Measures for Actuarial Applications" (Hardy), she describes as follows:

Using $H$ as a risk measure and $X$ as the associated risk distribution:

1. Translation Invariance

For any non-random $c$

\[H(X + c) = H(X) + c\]

This means that adding a constant amount (positive or negative) to a risk adds the same amount to the risk measure. It also implies that the risk measure for a non-random loss, with known value c, say, is just the amount of the loss c.

2. Positive Homogeneity

For any non-random $λ > 0$:

\[H(λX) = λH(X)\]

This axiom implies that changing the units of loss does not change the risk measure.

3. Subadditivity

For any two random losses $X$ and $Y$,

\[H(X + Y) ≤ H(X) + H(Y)\]

It should not be possible to reduce the economic capital required (or the appropriate premium) for a risk by splitting it into constituent parts. Or, in other words, diversification (ie consolidating risks) cannot make the risk greater, but it might make the risk smaller if the risks are less than perfectly correlated.

4. Monotonicity

If $Pr(X ≤ Y) = 1$ then $H(X) ≤ H(Y)$.

If one risk is always bigger then another, the risk measures should be similarly ordered.

Other Properties

In "Properties of Distortion Risk Measures" (Balbás, Garrido, Mayoral) also note other properties of interest:

Complete

Completeness is the property that the distortion function associated with the risk measure produces a unique mapping between the original risk's survival function $S(x)$ and the distorted $S*(x)$ for each $x$. See Distortion Risk Measures for more detail on this.

In practice, this means that a non-complete risk measure ignores some part of the risk distribution (e.g. CTE and VaR do not use the full distribution, so two risks that differ only outside the measured tail can produce the same value of the risk measure).

Exhaustive

A risk measure is "exhaustive" if it is coherent and complete.

Adaptable

A risk measure is "adapted" or "adaptable" if its distortion function (see Distortion Risk Measures) $g$ satisfies:

1. \[g\]

   is strictly concave, that is, $g^\prime$ is strictly decreasing.

2. \[\lim_{u\to 0^+} g^\prime(u) = \infty\]

   and $\lim_{u\to 1^-} g^\prime(u) = 0$.

Adaptive risk measures are exhaustive but the converse is not true.

Summary of Risk Measure Properties

Distortion Risk Measures

Distortion Risk Measures (Wikipedia Link) are a way of remapping the probabilities of a risk distribution in order to compute a risk measure $H$ on the risk distribution $X$.

Adapting Wang (2002), there are two key components:

Distortion Function $g(u)$

This remaps values in the [0,1] range to another value in the [0,1] range, and in $H$ below, operates on the survival function $S$ and $F=1-S$.

Let $g:[0,1]\to[0,1]$ be an increasing function with $g(0)=0$ and $g(1)=1$. The transform $F^*(x)=g(F(x))$ defines a distorted probability distribution, where "$g$" is called a distortion function.

Note that $F^*$ and $F$ are equivalent probability measures if and only if $g:[0,1]\to[0,1]$ is continuous and one-to-one. Definition 4.2. We define a family of distortion risk-measures using the mean-value under the distorted probability $F^*(x)=g(F(x))$:

Risk Measure Integration

To calculate a risk measure $H$, we integrate the distorted $F$ across all possible values in the risk distribution (i.e. $x \in X$):

\[H(X) = E^*(X) = - \int_{-\infty}^0 g(F(x))dx + \int_0^{+\infty}[1-g(F(x))]dx\]

That is, the risk measure ($H$) is equal to the expected value of the distortion of the risk distribution ($E^*(X)$).

Examples

Basic Usage

outcomes = rand(100)

# direct usage
VaR(0.90)(outcomes) # ≈ 0.90  
CTE(0.90)(outcomes) # ≈ 0.95  
WangTransform(0.90)(outcomes) # ≈ 0.81

# construct a reusable object (functor)
rm = VaR(0.90)

rm(outcomes) # ≈ 0.90

Comparison

We will generate a random outcome and show how the risk measures behave:

using Distributions
using ActuaryUtilities
using CairoMakie

outcomes = Weibull(1,5)
# or this could be discrete outcomes as in the next line
#outcomes = rand(LogNormal(2,10)*100,2000)

αs= range(0.00,0.99;length=100)

let
    f = Figure()
    ax = Axis(f[1,1],
        xlabel="α",
        ylabel="Loss",
        title = "Comparison of Risk Measures",
        xgridvisible=false,
        ygridvisible=false,
    )

    lines!(ax,
        αs,
        [quantile(outcomes, α) for α in αs],
        label = "Quantile α of Outcome",
        color = :grey10,
        linewidth = 3,
        )

    lines!(ax,
        αs,
        [VaR(α)(outcomes) for α in αs],
        label = "VaR(α)",
        linestyle=:dash
        )
    lines!(ax,
        αs,
        [CTE(α)(outcomes) for α in αs],
        label = "CTE(α)",
        )
    lines!(ax,
        αs[2:end],
        [WangTransform(α)(outcomes) for α in αs[2:end]],
        label = "WangTransform(α)",
        )
    lines!(ax,
        αs,
        [ProportionalHazard(2)(outcomes) for α in αs],
        label = "ProportionalHazard(2)",
        )

    lines!(ax,
        αs,
        [DualPower(2)(outcomes) for α in αs],
        label = "DualPower(2)",
        )
    lines!(ax,
        αs,
        [Expectation()(outcomes) for α in αs],
        label = "Expectation",
        )
    axislegend(ax,position=:lt)

        f
end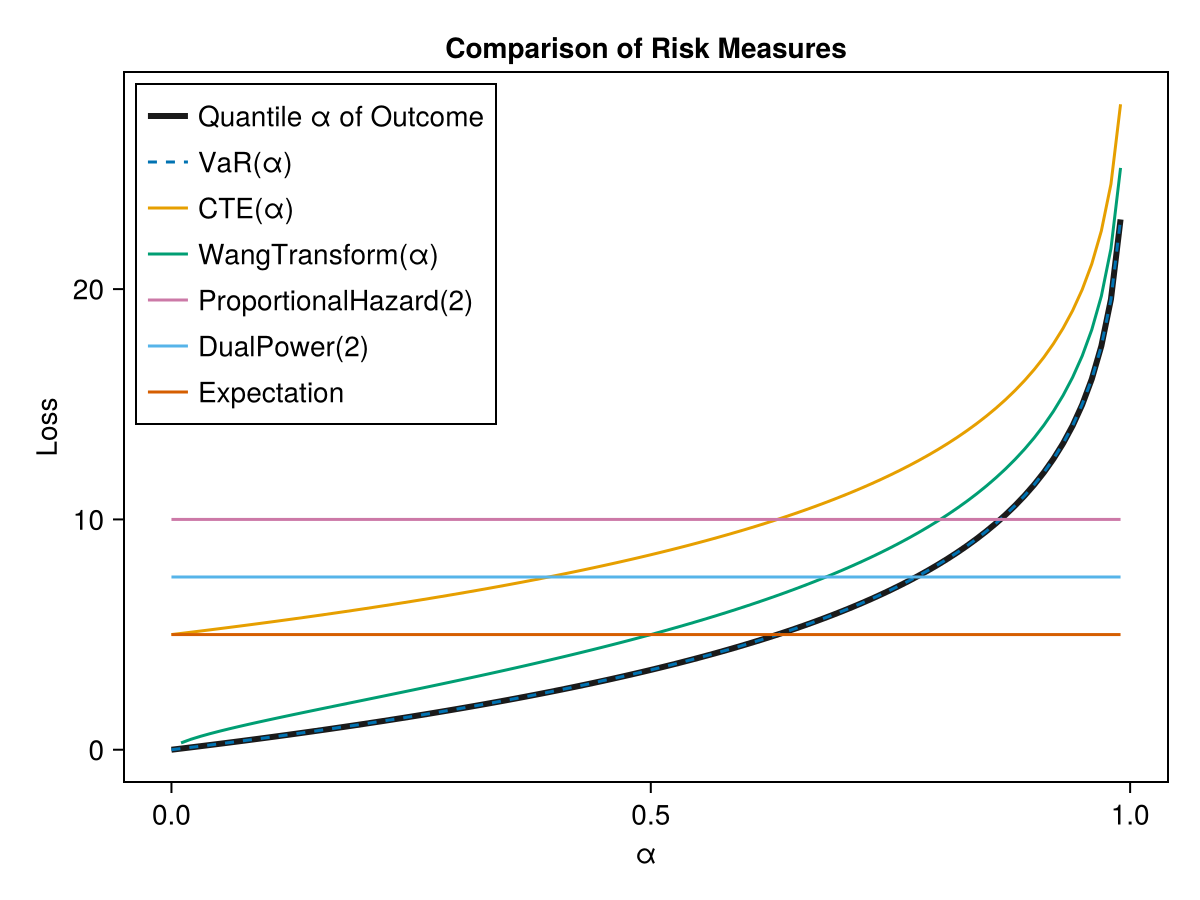

Optimal Transport & Robustness

A risk measure collapses a whole loss distribution to a single number. Optimal transport (OT) supplies the complementary half — the geometry between distributions: how far apart two risks are, how a rank-preserving stress moves every measure at once, whether a quarter-over-quarter change is real, and how much a risk measure can move under model error. In one dimension OT is closed form (transport is just rank matching), so these tools need no solver — they are sorting and quantile arithmetic layered on the same rm(risk) interface. For a broad treatment of optimal transport in an actuarial context, see Charpentier (2026), "Optimal Transport for Actuarial Science" ⟨hal-05684645⟩.

Distance between two risks — wasserstein

Where a risk measure says where a book sits, the Wasserstein distance says how far apart two books are, in the units of the loss and aware of the whole shape:

a = rand(LogNormal(log(1000) - 0.18, 0.6), 100_000)
b = rand(LogNormal(log(1150) - 0.32, 0.8), 100_000)   # higher mean + fatter tail

wasserstein(a, b)          # ≈ 210   average claim displacement (W₁, in \$)
wasserstein(a, b; p=2)     # ≈ 480   W₂ penalizes the tail move more

It also accepts Distributions.UnivariateDistributions directly, e.g. wasserstein(Normal(0, 1), Normal(3, 1)) == 3.

One stress drives the whole panel — transportmap / pushforward

Rather than stressing each measure separately, define one rank-preserving transport map, push the book through it, and recompute every measure consistently:

base_law = LogNormal(log(1000) - 0.18, 0.6)                    # the assumed base
T        = transportmap(base_law, LogNormal(log(1300) - 0.32, 0.8))  # → target
sample   = rand(base_law, 100_000)
stress   = pushforward(sample, T)

for rm in (Expectation(), VaR(0.95), CTE(0.95), VaR(0.995), CTE(0.995))
    println(rm, ": ", round(rm(sample)), " → ", round(rm(stress)))
end

The map is auditable ("we revalued each percentile") rather than a reshuffling of who is risky.

Distributionally robust risk measures — robustvalue

robustvalue(rm, sample; radius=r) is a robust version of rm over a Wasserstein ball of radius r — a governance dial in the units of the loss for "how bad could this number be if my book is off by up to r of transport cost?" For CTE(α) it is the exact worst case, attaining the sharp stability bound $|\mathrm{CTE}_\alpha(\mu)-\mathrm{CTE}_\alpha(\nu)| \le (1-\alpha)^{-1/p}\,W_p$; for every other measure it evaluates rm on a budget-exact adverse scenario inside the ball, which is a lower bound on the true worst case — a distinction that matters if the number feeds capital or model-risk governance:

base = rand(LogNormal(log(1000) - 0.18, 0.6), 200_000)

CTE(0.95)(base),  robustvalue(CTE(0.95),  base; radius=250)   # ≈ (2980, 4100)
CTE(0.995)(base), robustvalue(CTE(0.995), base; radius=250)   # ≈ (4890, 8430)

Same $250 radius, a larger loading deeper in the tail — deep-tail capital is intrinsically more fragile to model error. Because robustvalue takes the risk measure as an argument it works for VaR, WangTransform, or any custom RiskMeasure (pass tail for measures without a natural tail level).

Is a change real? — a worked example (deliberately not API)

A risk number that moved quarter-to-quarter may just be sampling noise. Deciding whether the move is real is a modelling judgement — the test level, the prior, and the materiality threshold all belong in your hands, not baked into a library primitive — so this package ships the distance primitive (wasserstein) and leaves the drift check as a few lines of user code. Both standard treatments fit in a screenful.

Frequentist screen (permutation test). Pool the two samples and re-split them at random many times: the re-split distances are what "no drift" looks like at your sample size, and only an observed distance that clears that noise floor is worth escalating. Seed the rng — the floor is stochastic, and a figure of record must be reproducible:

using ActuaryUtilities, Distributions, Random, Statistics

rng = Xoshiro(2026)
q1 = rand(rng, LogNormal(log(1000) - 0.18, 0.60), 4_000)   # this quarter
q2 = rand(rng, LogNormal(log(1030) - 0.19, 0.62), 4_000)   # next quarter

function drift_permutation(a, b; p=1, nperm=1000, level=0.9, rng=Xoshiro(2026))
    observed = wasserstein(a, b; p)
    pool, na = vcat(a, b), length(a)
    resplit = map(1:nperm) do _
        s = shuffle(rng, pool)
        wasserstein(view(s, 1:na), view(s, na+1:lastindex(s)); p)
    end
    (; observed,
        threshold=quantile(resplit, level),                     # the noise floor
        pvalue=(count(>=(observed), resplit) + 1) / (nperm + 1),
        resplit)                                                # the null draws, for plotting
end

res = drift_permutation(q1, q2)
(; res.observed, res.threshold, res.pvalue)

(observed = 37.78989612401512, threshold = 29.537321259885285, pvalue = 0.028971028971028972)

The returned resplit vector is the null distribution — the first thing to do with a borderline result is plot it against observed, so the recipe hands it back rather than making you re-run the permutations. And the default level=0.9 is a screening threshold; raise it for anything feeding a decision.

Generative effect size (a Turing model). The committee question is usually not "is there any drift?" but "how big is it, why, and is it past materiality?" — an effect-size statement about the laws, not the samples. Write a generative model of the two periods (here lognormal severities with a location drift δ and per-period dispersions — the priors and the likelihood are exactly the judgement calls that belong to you), then push the joint posterior through the same wasserstein primitive, now between fitted laws:

using Turing

@model function severity_drift(x1, x2)
    μ  ~ Normal(log(1000), 1)                  # baseline log-severity location
    δ  ~ Normal(0, 0.25)                       # location drift (≈ % severity trend)
    σ1 ~ truncated(Normal(0.6, 0.3); lower=0)  # baseline dispersion
    σ2 ~ truncated(Normal(0.6, 0.3); lower=0)  # next-quarter dispersion
    x1 ~ filldist(LogNormal(μ, σ1), length(x1))
    x2 ~ filldist(LogNormal(μ + δ, σ2), length(x2))
end

chain = sample(Xoshiro(2026), severity_drift(q1, q2), NUTS(), 1_000)
μs  = vec(collect(chain[@varname(μ)]))
δs  = vec(collect(chain[@varname(δ)]))
σ1s = vec(collect(chain[@varname(σ1)]))
σ2s = vec(collect(chain[@varname(σ2)]))

# posterior over the drift distance between LAWS — the same wasserstein verb:
Wpost = [wasserstein(LogNormal(μ, σ1), LogNormal(μ + δ, σ2))
         for (μ, δ, σ1, σ2) in zip(μs, δs, σ1s, σ2s)]

quantile(Wpost, [0.05, 0.5, 0.95])   # credible band for the drift, in \$
mean(Wpost .> 40)                    # P(drift > \$40 materiality) — the governance question

This buys three things a distance between raw samples cannot. The sampling noise is integrated out rather than carried along — the plug-in distance between two finite samples of the same law is strictly positive, so a sample-based posterior is biased upward, while the model's posterior is a statement about the laws themselves. (One behavior to expect even so: a distance is nonnegative, so on a stable book the posterior of Wpost does not collapse to zero — parameter wiggle folds into a materially positive median. Read the signed δ and σ2 - σ1 posteriors and the materiality probability, not the distance median alone.) The parameters decompose the why: a δ posterior straddling zero alongside a σ2 - σ1 posterior that excludes it reads "severity isn't trending — the distribution is widening," which points at volatility or mix rather than inflation, and different causes demand different actions. And every tail statement becomes a statement about a law with honest parameter uncertainty — CTE(0.995)(LogNormal(μ + δ, σ2)) per draw — extrapolated through the fitted form instead of read off the worst handful of observations. The price is symmetric: those answers are conditional on the model, so before trusting them, check the fit (simulate from the priors before fitting; after fitting, compare posterior-predictive draws against the empirical tail quantiles). A misspecified likelihood will confidently describe a book that doesn't exist.

The two recipes answer different questions — "could this be noise?" versus "how big is it, why, and with what uncertainty?" — and a governance process often wants the permutation screen first and the generative effect-size statement for anything that passes.

Discussion: how to read these numbers, and what is deliberately left out

Every exported verb above is objective — sorting and quantile arithmetic with no priors, no tuning knobs, and no solver. That is what keeps them auditable and exactly reproducible, and it is a deliberate scope choice. The drift check is the place where judgement necessarily enters, which is exactly why it is a worked example rather than an export.

A permutation test is a calibration, not a probability that the book changed. The permutation screen's implied null hypothesis is that the two periods are drawn from exactly the same law. In practice that null is never literally true — books always drift a little — so a "significant" result really tells you the samples were large enough to detect some change, not that the change is material. The pvalue is P(distance this large | no drift), which is easy to misread as P(drift is real | data); they are not the same number, and in a governance setting the misread is the default. The noise floor exists for a concrete reason: the plug-in Wasserstein distance is biased upward in finite samples — wasserstein(x, y) between two samples of the same law is positive, not zero — so the permutation floor is best understood as a bias correction for that estimator rather than as a hypothesis-testing ritual.

What the generative (Bayesian) view adds. The question a capital or experience committee usually wants answered is not "is there any drift?" but "how big is the drift, why, with what uncertainty, and is it past a materiality threshold?" — a statement about effect size and mechanism, not a point-null rejection. The Turing model above targets that directly, and a fuller treatment can go further: hierarchical structure borrowing information across a history of quarters and blocks, covariates and censoring/truncation in the likelihood, and handling the many-blocks, many-quarters multiplicity that makes any fixed-threshold flag trip on a predictable fraction of stable books. None of this is exported API on purpose: the test level, the priors, the likelihood, and the materiality threshold are modelling choices that belong in the user's hands, and the permutation screen and a generative posterior answer genuinely different questions (a calibration reference versus effect-size uncertainty conditional on a model you must check). Treat any boolean "significant" flag as a screen, not a conclusion, and pin a seeded rng for any figure of record.

Multivariate risks need a solver. Everything here is one-dimensional, where optimal transport is closed form (transport is rank matching). Genuinely joint risks — mortality × lapse, equity × rates, several lines of business at once — are not: in more than one dimension the transport map is no longer a sorted matching and requires an actual OT solve. That capability is a natural future extension (dispatched on multivariate inputs, lit up when a package such as OptimalTransport.jl is loaded), and it is a real addition rather than a re-wrapping of the exact 1-D routines. Note that robustvalue does not generalize for free: its "shift the tail mass outward by Δ" form is intrinsically a one-dimensional tail result, and the multivariate worst case over a Wasserstein ball is a separate optimization problem.

API

Exported API

CTE(α)::RiskMeasure
CTE(α)(risk)::T (where T is the type of values sampled in risk)

julia> CTE(0.95)(rand(1000))
0.9766218612020593

julia> rm = CTE(0.95)
CTE{Float64}(0.95)

julia> rm(rand(1000))
0.9739835010268733

DualPower(v)::RiskMeasure
DualPower(v)(risk)::T (where T is the type of values sampled in risk)

Expectation()::RiskMeasure
Expectation()(risk)::T (where T is the type of values sampled in `risk`)

julia> Expectation()(rand(1000))
0.4793223308812537

julia> rm = Expectation()
ActuaryUtilities.RiskMeasures.Expectation()

julia> rm(rand(1000))
0.4941708036889741

ProportionalHazard(y)::RiskMeasure
ProportionalHazard(y)(risk)::T (where T is the type of values sampled in risk)

julia> ProportionalHazard(2)(rand(1000))
0.6659603556774121

julia> rm = ProportionalHazard(2)
ProportionalHazard{Int64}(2)

julia> rm(rand(1000))
0.6710587338367799

 VaR(α)::RiskMeasure
 VaR(α)(risk)::T (where T is the type of values sampled in `risk`)

julia> VaR(0.95)(rand(1000))
0.9561843082268024

julia> rm = VaR(0.95)
VaR{Float64}(0.95)

julia> rm(rand(1000))
0.9597070153670079

WangTransform(α)::RiskMeasure
WangTransform(α)(risk)::T (where T is the type of values sampled in risk)

julia> WangTransform(0.95)(rand(1000))
0.8799465543360105

julia> rm = WangTransform(0.95)
WangTransform{Float64}(0.95)

julia> rm(rand(1000))
0.8892245759705852

pushforward(sample, T)

robustvalue(rm::RiskMeasure, sample; radius, p=2, tail=<rm's α>)

julia> s = rand(LogNormal(log(1000) - 0.18, 0.6), 200_000);

julia> CTE(0.95)(s), robustvalue(CTE(0.95), s; radius=250)   # ≈ (2980, 4100)

transportmap(source, target)

julia> T = transportmap(Normal(0, 1), Normal(3, 1));  # a rigid +3 shift

julia> T(0.0), T(1.0)
(3.0, 4.0)

wasserstein(a, b; p=1, rtol=1e-6, atol=0, maxevals=nothing)

julia> wasserstein([1, 2, 3], [4, 5, 6])            # a rigid $3 shift
3.0

julia> wasserstein(Normal(0, 1), Normal(3, 1))      # translation ⇒ W_p = 3
3.0

julia> wasserstein(Normal(0, 1), Normal(0, 2); p=2) # same mean, |σ₁-σ₂|
1.0

Unexported API

cdf_func(risk)

cdf_func(S::AbstractArray{<:Real}) = StatsBase.ecdf(S)
cdf_func(S::Distributions.UnivariateDistribution) = x -> Distributions.cdf(S, x)

g(rm::RiskMeasure,x)